
Igrajte Futoshiki Puzzles online
U sljedećem vodiču, osnovne i napredne tehnike rješavanja Futoshiki zagonetki prikazane su korak po korak, s pratećim ilustracijama koje prikazuju metode na specifičnim konfiguracijama ploče.
Polazna točka za postizanje rješenja je sama definicija igre: Futoshiki zahtijeva od korisnika da pronađe ploču na kojoj se svaka znamenka pojavljuje jednom u svakom retku i stupcu, poštujući nejednakosti ploče. Korištenjem ovog kriterija, napredak prema rješenju može se postići popunjavanjem, korak po korak, praznih polja ploče određenim znamenkama jer su to jedini način da se poštuju ograničenja ploče.
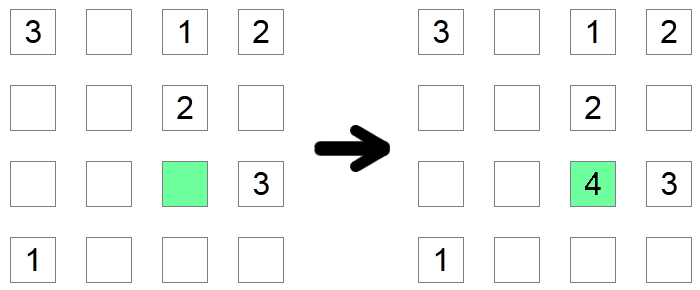
Ako stupac i redak kvadrata već sadrže sve moguće znamenke osim jedne, tada taj kvadrat mora sadržavati nedostajuću znamenku. U gornjem primjeru, zeleni kvadrat mora biti 4 jer ne bi smio imati nijednu drugu vrijednost jer se ostale moguće znamenke već nalaze u njegovom retku ili stupcu.
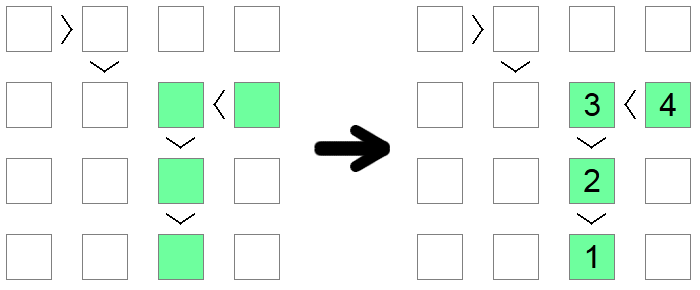
Ako primijetite lanac nejednakosti, bilo da je < (sve rastuće) ili > (sve silazno), jednake veličine kao i veličina ploče, tada taj lanac mora biti niz od 1 do duljine ploče. Duljina lanca jamči da je taj niz jedino moguće rješenje koje zadovoljava uvjet monotonosti nametnut lancem nejednakosti.
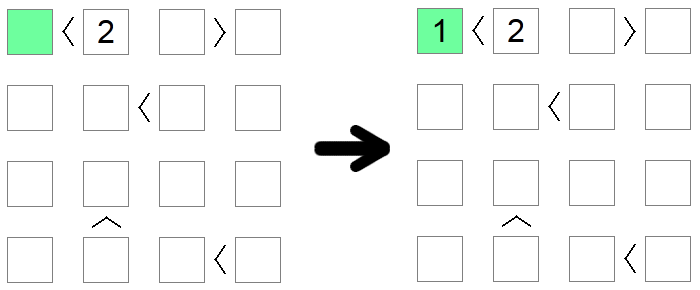
Polja koja su manja od 2 moraju implicitno imati vrijednost 1 jer je to jedina dopuštena vrijednost na ploči koja poštuje taj uvjet. Slično tome, polja koja su veća od veličine ploče minus 1 moraju biti jednaka veličini ploče. U gornjem primjeru, jedina moguća vrijednost za zeleno polje (manje od 2) je 1 .
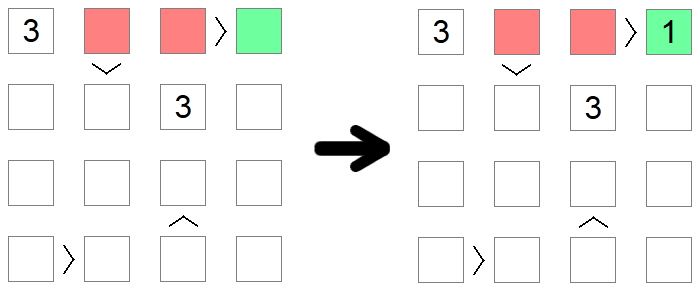
Kvadrati koji su veći od drugih kvadrata ne mogu biti 1 , najniža dopuštena vrijednost na ploči, jer ne postoji vrijednost manja od 1. Slično tome, kvadrati koji su manji od drugih kvadrata ne mogu sadržavati maksimalnu dopuštenu vrijednost, jer ne bi bilo ništa veće za popunjavanje na drugoj strani nejednakosti. U gornjem primjeru, 1 se ne može popuniti u crvenim kvadratima jer su svi veći od ostalih kvadrata na ploči, pa je jedini mogući položaj za 1 u prvom redu ploče zeleni kvadrat.
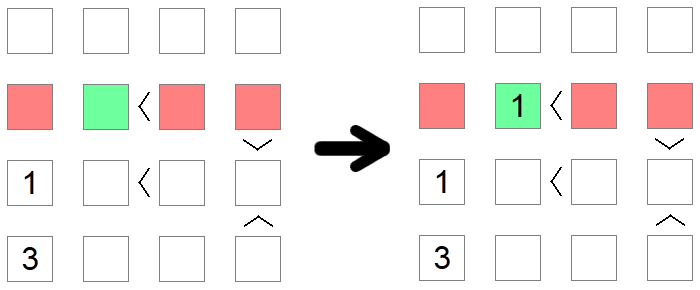
Ponekad se mora koristiti više pravila kako bi se došlo do zaključka. To je slučaj u gornjem primjeru, gdje pokušavamo smjestiti vrijednost 1 u drugi red ploče. Prvi crveni kvadrat se eliminira zbog isključenja stupca (već imamo 1 u tom stupcu), dok se drugi i treći crveni kvadrat eliminiraju zbog isključenja minimalnih vrijednosti jer ta mjesta imaju nejednakosti 'veće od' povezane s njima. Stoga zeleni kvadrat ostaje jedino moguće mjesto za postavljanje 1 u tom redu.
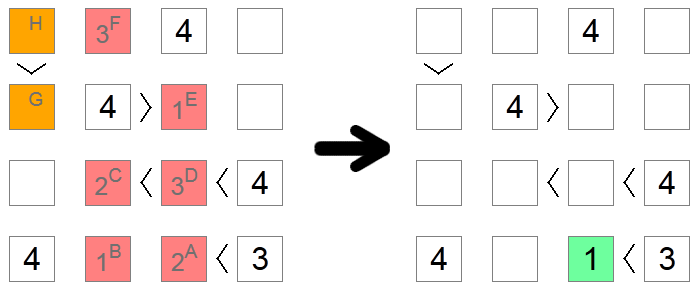
Ponekad, posebno na teškim pločama, ne postoje drugi načini za određivanje točne znamenke za kvadrat osim istraživanja implikacija svake mogućnosti dok se ne dođe do kontradikcije. U gornjem primjeru, sva crvena i narančasta polja su u početku prazna. Želimo saznati sadrži li kvadrat A 1 ili 2. Pretpostavljamo da sadrži 2 i provjeravamo dolazimo li do kontradikcije na temelju te pretpostavke.
Ako kvadrat A ima 2 , tada bi kvadrat B imao 1 (jedina preostala vrijednost u donjem retku). Kvadrat C može biti 1 ili 2 jer ima lanac nejednakosti koji zahtijeva dostupnost 2 veća broja, ali sada ne može biti 1 zbog isključenja stupca kvadrata B, pa je kvadrat C 2 , a kvadrat D je 3 (jedina vrijednost između 2 i 4). Zbog isključenja stupaca, kvadrat E je 1, a kvadrat F je 3 .
Sada, ako pogledamo narančaste kvadrate, uočavamo kontradikciju: ako bi kvadrat G bio 2, kvadrat H morao bi biti 3 ili 4, što nije dopušteno zbog isključenja retka. Ako bi kvadrat G bio 3, kvadrat H morao bi biti 4, što nije dopušteno iz istog razloga. Budući da više nemamo preostalih vrijednosti za kvadrat G, to znači da smo došli do zastoja i naša početna pretpostavka bila je pogrešna: 2 nije valjan potez za kvadrat A, pa možemo nastaviti i staviti 1 u njega, jedinu drugu moguću vrijednost.
Gore smo pokazali kako uspješno riješiti Futoshiki zagonetku pokrivajući niz tehnika koje vam mogu pomoći da odredite sljedeći potez čak i u teškim situacijama. Drugi ključni sastojak za vješto i brzo rješavanje Futoshiki zagonetki je iskustvo: što više vježbate, to ćete postati bolji i brži.
Ako ste spremni za izazov, možete odmah igrati nasumične Futoshiki zagonetke klikom na gumb ispod. Sretno!
© 2026 - Sva prava pridržana - Oko - Pravila o privatnosti - DA | DE | EN | ES | ET | FI | FR | HR | IT | LT | LV | NL | PL | PT | RO | SV | TR